前に見たように,テイラー展開はある点を基準とした局所的な級数展開でした.それゆえ,例えば下図のような周期的な関数の展開には不向きです.
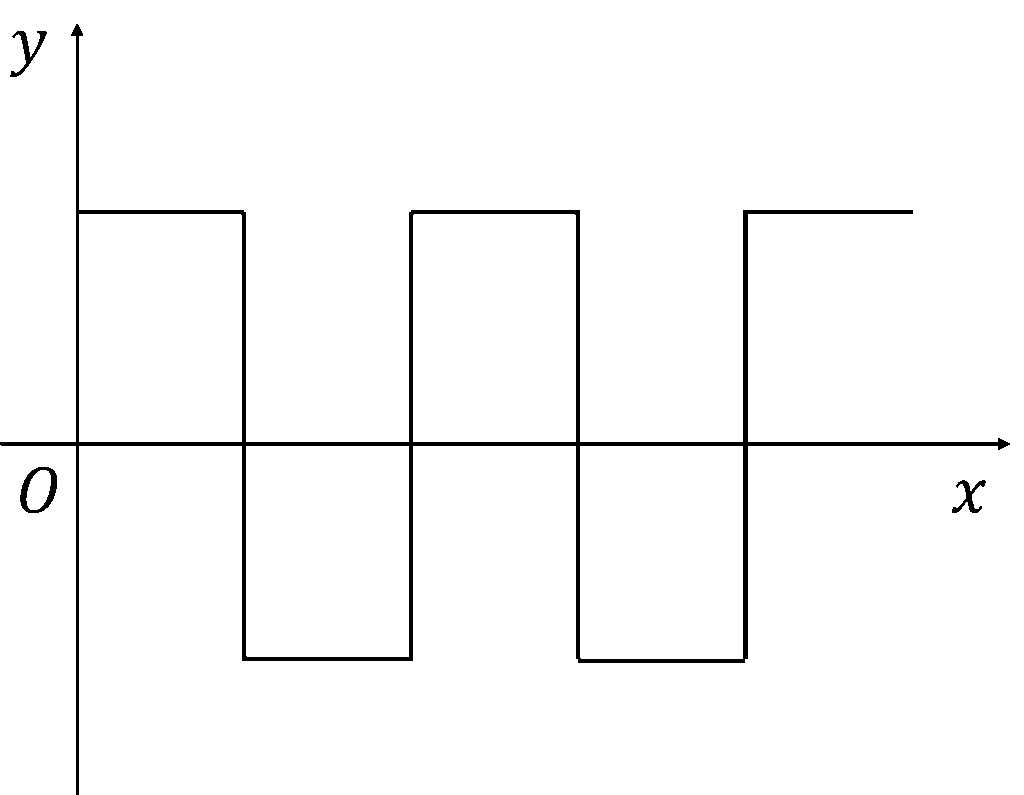
このような周期的な関数を級数展開したい場合は,同じ周期関数を用いた大局的な展開が必要となります.これを考えていきましょう.
まず,適当な周期関数として思いつくのは\(\sin\)もしくは\(\cos\)でしょう(\(\tan\)は不連続であるので,扱いにくい).また,奇関数である\(\sin\)は奇関数のみ,偶関数である\(\cos\)は偶関数のみ表現でき,一方が他方を表現することはできないことを考えれば,一般の場合においては\(\sin\)と\(\cos\)両方要することになります.さらに,元の関数の周期を崩さずに展開するには,級数を構成する\(\sin\)および\(\cos\)がその周期でぴったりと収まればよく,たとえば\(\sin\)は
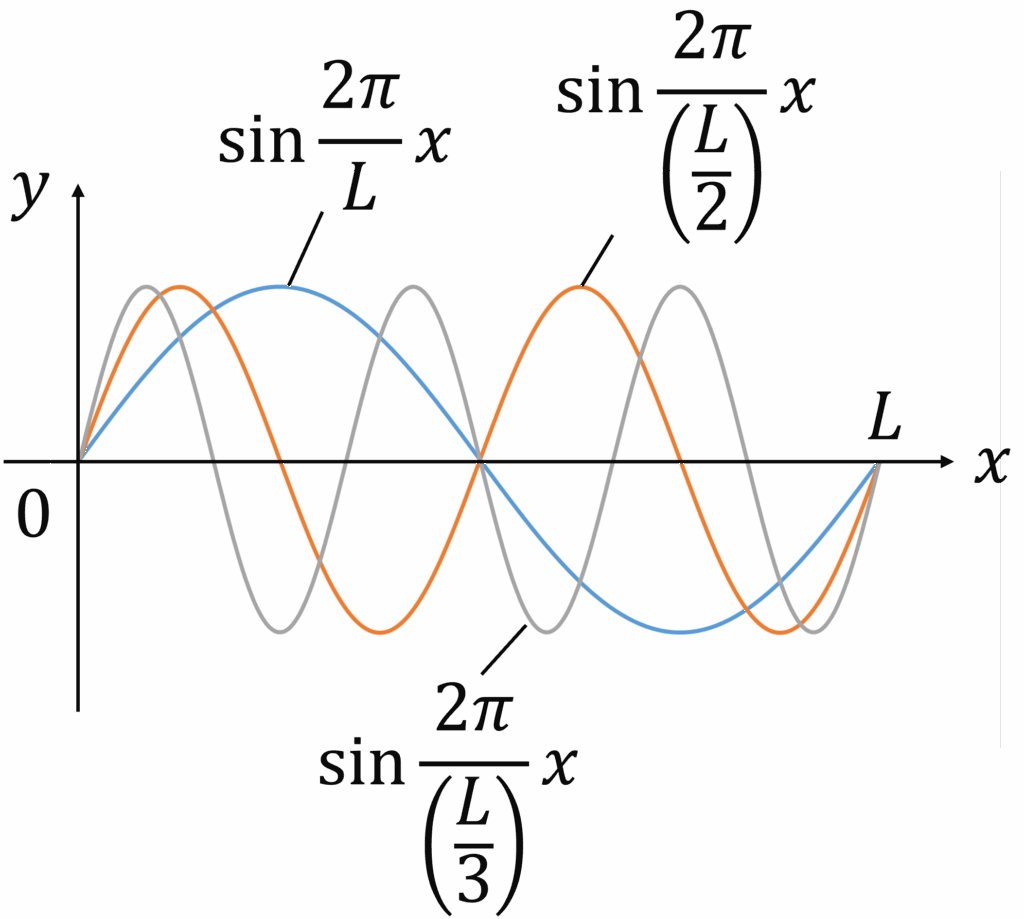
のように周期が1/整数倍,すなわち位相が整数倍となるものは同じ周期でぴったりと収まることが分かります(\(\cos\)も同様).そこで,周期\(L\)の関数\(f(x)\)について,ひとまず\[f(x)=a_0+(a_1\sin \frac{2π}{L}x+b_1\cos \frac{2π}{L}x)+(a_2\sin \frac{4π}{L}x+b_2\cos \frac{4π}{L}x)+(a_3\sin \frac{6π}{L}x+b_3\cos \frac{6π}{L}x)+・・・+(a_k\sin \frac{2πk}{L}x+b_k\cos \frac{2πk}{L}x)+・・・\]と展開できるものとします.この展開を求めるには,各項の係数\(a_0,(a_1,b_1),(a_2,b_2),・・・\)を求めればよいので,順次これらの係数を求めていくことにします.この際,重要な三角関数の性質として,直交性\[\int_{0}^{L}\sin (\frac{2πk}{L}x)\sin (\frac{2πn}{L}x)dx=\begin{Bmatrix}
0(k≠n) \\
\frac{L}{2}(k=n≠0)\end{Bmatrix}\]\[\int_{0}^{L}\cos (\frac{2πk}{L}x)\cos (\frac{2πn}{L}x)dx=\begin{Bmatrix}
0(k≠n) \\
\frac{L}{2}(k=n≠0)\end{Bmatrix}\]\[\int_{0}^{L}\sin (\frac{2πk}{L}x)\cos (\frac{2πn}{L}x)dx=0\]を用います\((k,nは自然数)\).
まず,与式を\(0からL\)まで積分すれば\[\int_{0}^{L}f(x)dx=\int_{0}^{L}a_0dx=La_0\qquad ∴a_0=\frac{1}{L}\int_{0}^{L}f(x)dx\]を得ます.次に,\(\sin\)の係数を得るために与式に\(\sin \frac{2πn}{L}x\)をかけ,\(0からL\)まで積分すれば\[\int_{0}^{L}f(x)\sin \frac{2πn}{L}xdx=\sum_{k=1}^{∞}\int_{0}^{L}a_k\sin \frac{2πk}{L}x\sin\frac{2πn}{L} xdx=\frac{L}{2}a_k\qquad ∴a_k=\frac{2}{L}\int_{0}^{L}f(x)\sin\frac{2πk}{L} xdx\qquad (k=n)\]を得る.同様に,\(\cos\)の係数を得るために与式に\(\cos \frac{2πn}{L}x\)をかけ,\(0からL\)まで積分すれば\[\int_{0}^{L}f(x)\cos \frac{2πn}{L}xdx=\sum_{k=1}^{∞}\int_{0}^{L}b_k\cos \frac{2πk}{L}x\cos\frac{2πn}{L} xdx=\frac{L}{2}b_k\qquad ∴b_k=\frac{2}{L}\int_{0}^{L}f(x)\cos\frac{2πk}{L} xdx\qquad (k=n)\]を得ます.こうして,各項の係数が定まり,級数を求めることができます.これをフーリエ級数展開といいます.例として,周期\(L\)の方形波\[f(x)=\begin{Bmatrix}
1 \qquad (0<x<\frac{L}{2})\\
-1 \qquad (\frac{L}{2}<x<L)\end{Bmatrix}\]のフーリエ級数展開を考えると,係数についてまず定数項は\[a_0=\frac{1}{L}(\int_{0}^{\frac{L}{2}}1dx+\int_{\frac{L}{2}}^{L}(-1)dx)=0\]であり,\(\sin\)成分は\[a_k=\frac{2}{L}(\int_{0}^{\frac{L}{2}}\sin\frac{2πk}{L} xdx+\int_{\frac{L}{2}}^{L}(-1)\sin\frac{2πk}{L} xdx)=\frac{4}{kπ}(1-\cos kπ)\]となります.また\(f(x)\)は奇関数なので\(\cos\)成分は0となります.したがって,与式は\[f(x)=\sum_{k=1}^{∞}\frac{4}{kπ}(1-\cos kπ)\sin \frac{2πk}{L}x=\frac{8}{π}\sin \frac{2π}{L}x+\frac{8}{3π}\sin \frac{4π}{L}x+\frac{8}{5π}\sin \frac{10π}{L}x・・・\]と展開できます.いま,もとの波形と9項までの級数展開の結果を比べると,下図のようになります.
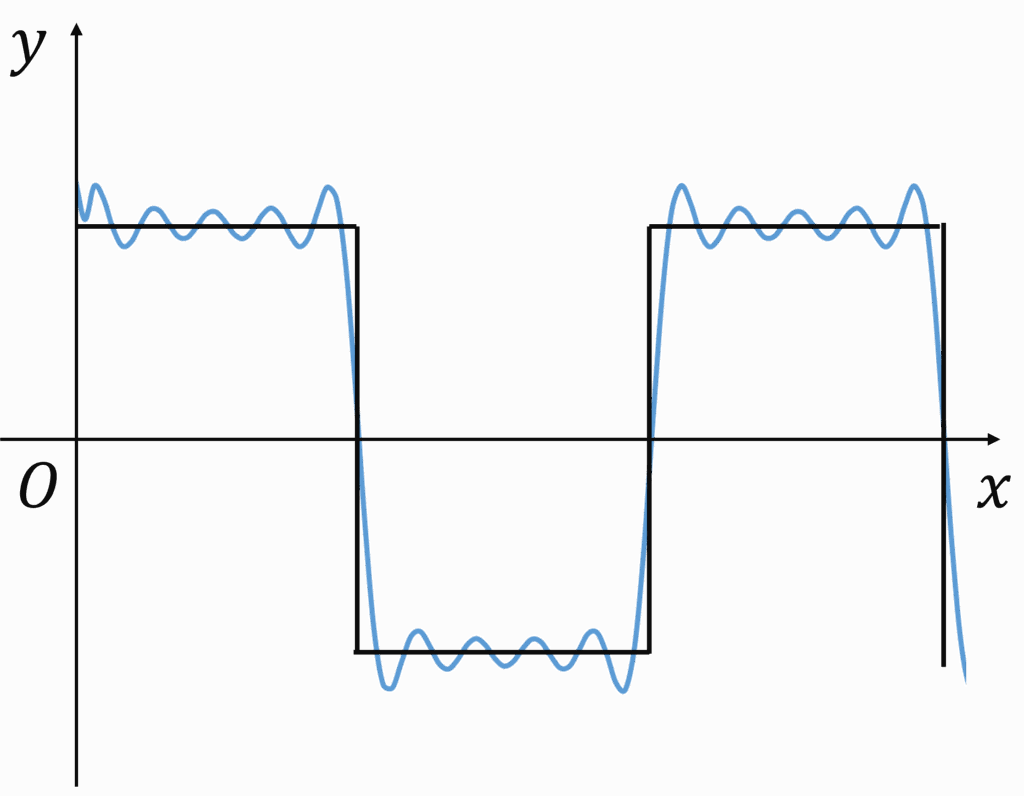
このように,フーリエ級数展開は,大きさと位相の異なる三角関数を足し合わせることによりもとの関数を近似する方法と言えます.