物理学や工学では,現象を表現するために様々な関数を用います.しかし,それらを解析する際,関数そのままの形では取り扱いが難しいことが往々にしてあります.このような関数を級数という比較的取り扱いやすい形式に展開する方法について考えてみます.
いま,ある関数\(f(x)\)が\[f(x)=a_0x^0+a_1x^1+a_2x^2+a_3x^3+a_4x^4+・・・+a_kx^k+・・・\]というような級数に展開できたとします.ただし,\(f(x)\)は何回でも微分をすることができるものとします.この展開を求めるには,各項の係数\(a_0,a_1,a_2,・・・\)を求めればよいので,順次これらの係数を求めていくことにします.まず,与式に\(x=0\)を代入すれば\[f(0)=a_0\]より,係数a_0が求まりました.次に,与式の両辺を\(x\)で繰り返し微分していいくと\[f(x)^{(1)}=a_1+2a_2x^1+3a_3x^2+4a_4x^3・・・+ka_kx^{k-1}+・・・\]\[f(x)^{(2)}=2a_2+3\cdot2a_3x^1+4\cdot3a_4x^2+・・・+k(k-1)a_kx^{k-2}+・・・\]\[f(x)^{(3)}=3\cdot2a_3+4\cdot3\cdot2a_4x^1・・・+k(k-1)(k-2)a_kx^{k-3}+・・・\]\[\vdots\]となり,それぞれ\(x=0\)とすれば\[f(0)^{(1)}=a_1=1!a_1\]\[f(0)^{(2)}=2a_2=2!a_2\]\[f(0)^{(3)}=3\cdot2a_3=3!a_3\]\[\vdots\]より,各項の係数を求めることができます.したがって,与式は\[f(x)=f(0)+\frac{f(0)^{(1)}}{1!}x^1+\frac{f(0)^{(2)}}{2!}x^2+\frac{f(0)^{(3)}}{3!}x^3+・・・+\frac{f(0)^{(k)}}{k!}x^k+・・・\]と展開することができます.これをマクローリン展開といいます.例として,\(\sin x\)のマクローリン展開を見てみましょう.マクローリン展開の式に従って展開すれば\[\sin x=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}+・・・\]となります.このように,\(\sin x\)のような一般の関数も,何回も微分可能である場合においてはべき級数に展開できることが分かります.また,\(f0=x,f3=x-\frac{x^3}{3!},f5=x-\frac{x^3}{3!}+\frac{x^5}{5!},f7=x-\frac{x^3}{3!}+\frac{x^5}{5!}-\frac{x^7}{7!}\)として,級数の項を増やしていった際の様子をグラフにすると,下図のようになります.
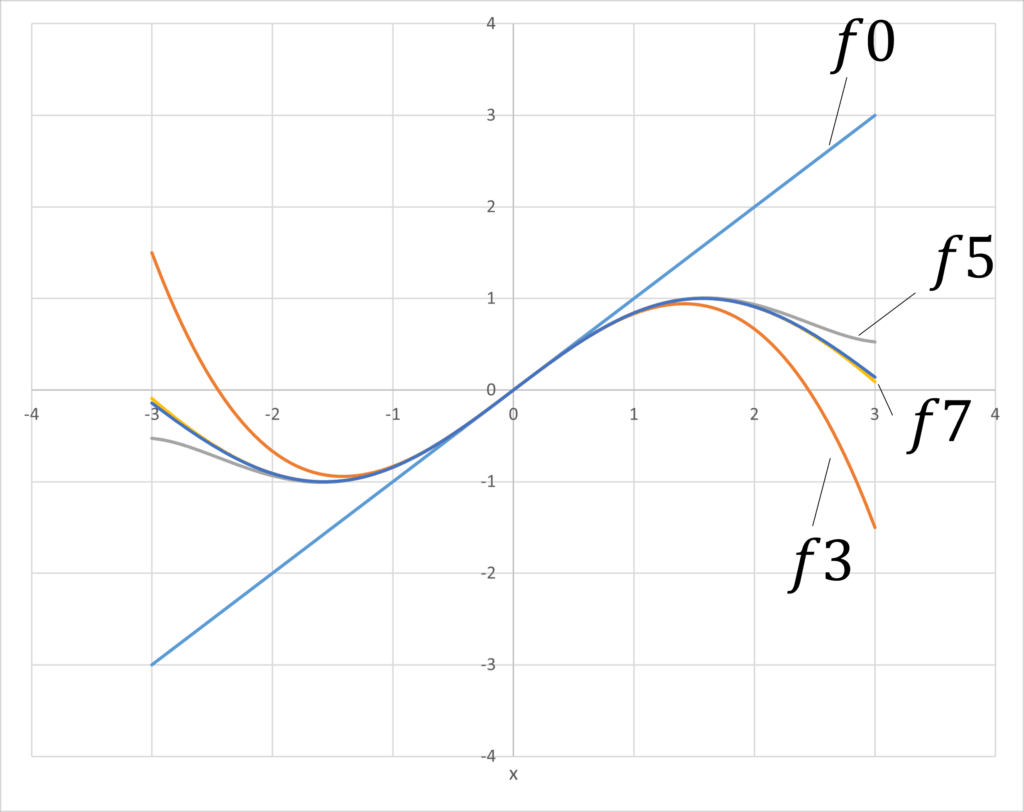
図より,\(x=0\)の付近において,級数の項が増えるほど元の形(\(\sin x\))に近づいていくことが分かります.このように,マクローリン展開は\(x=0\)の付近で関数を近似し,級数の項を増やすことによって近似の精度を高める方法と言えます.
マクローリン展開は,\(x=0\)の付近で展開を行い,近似を求める方法でした.これに対して,任意の位置\(x=x_0\)の付近で展開を行いたい場合は,はじめに関数の展開が\[f(x)=a_0(x-x_0)^0+a_1(x-x_0)^1+a_2(x-x_0)^2+a_3(x-x_0)^3+a_4(x-x_0)^4+・・・+a_k(x-x_0)^k+・・・\]と展開できると考えて,マクローリン展開のときと同様にすれば\[f(x)=f(x_0)+\frac{f(x_0)^{(1)}}{1!}(x-x_0)^1+\frac{f(x_0)^{(2)}}{2!}(x-x_0)^2+\frac{f(x_0)^{(3)}}{3!}(x-x_0)^3+・・・+\frac{f(x_0)^{(k)}}{k!}(x-x_0)^k+・・・\]が成り立ちます.これを\(x=x_0\)周りでのテイラー展開といい,\(x=x_0\)の付近で関数を近似し,級数の項を増やすことによって近似の精度を高める方法と言えます.実際,\(\sin x\)を\(x=1.5\)周りでテイラー展開すると\[\sin 1.5+\frac{\cos 1.5}{1!}(x-1.5)^1-\frac{\sin 1.5}{2!}(x-1.5)^2-\frac{\cos 1.5}{3!}(x-1.5)^3+・・・\]となり,いま\(f0=\sin 1.5,f1=\sin 1.5+\frac{\cos 1.5}{1!}(x-1.5)^1,f2=\sin 1.5+\frac{\cos 1.5}{1!}(x-1.5)^1-\frac{\sin 1.5}{2!}(x-1.5)^2,f3=\sin 1.5+\frac{\cos 1.5}{1!}(x-1.5)^1-\frac{\sin 1.5}{2!}(x-1.5)^2-\frac{\cos 1.5}{3!}(x-1.5)^3\)として,級数の項を増やしていった際の様子をグラフにすると,下図のようになります.
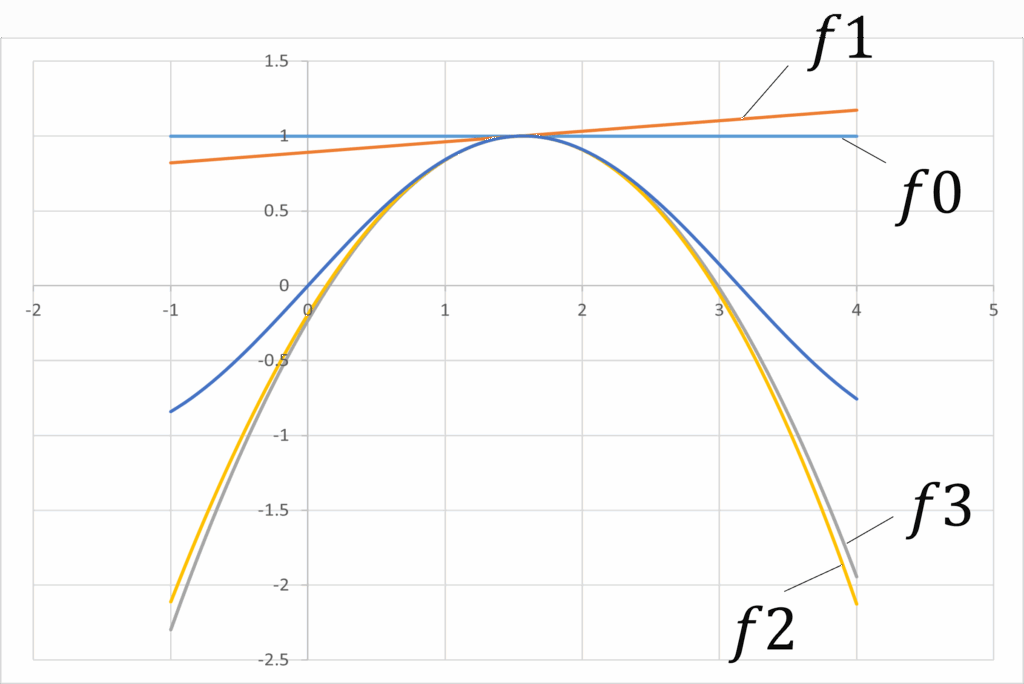
図より,\(x=1.5\)の付近において,級数の項が増えるほど元の形(\(\sin x\))に近づいていくことが分かります.このように,マクローリン展開やテイラー展開は,ある\(x\)の付近において,関数を近似したいときに強力な武器となります.なお,マクローリン展開はテイラー展開において\(x_0=0\)と置いたものと解釈できるので,テイラー展開の特別な場合と考えられます.