自然現象は,物理量の時間的変化によってもたらされ,その変化の指標として導関数が導入されます.例えば,位置\(x\)が時間\(t\)に伴って変化するとき,位置の導関数すなわち速度は\[v(t)=\frac{dx}{dt}\]と表されます.では逆に,速度の情報が与えられた際に位置はどのように求められるのでしょうか.
まず簡単に,ある物体の速度が\(v=一定\)であるとすれば,時間\(Δt\)の間に物体が動く距離\(Δx\)は速度の定義式より\[v=\frac{Δx}{Δt}\qquad ∴ Δx=vΔt\]となります.すなわち,速度が一定である場合,速度と時間をかけ合わせることでその間の変位が得られることになります.これは,下図のような\(v-t\)グラフにおける面積で与えられることがわかります.

では,より一般に下図のように速度が時間の経過に伴って変化する場合,変位はどのように計算すればよいでしょうか.
このように複雑な図形の面積を求める公式はありません.そこで,一つの発想として区間を細かく分割することを考えてみます.すると,下図のように細切れ一つ当たりの幅が小さいことにより,その間の速度をほぼ一定とみなすことができるようになります.
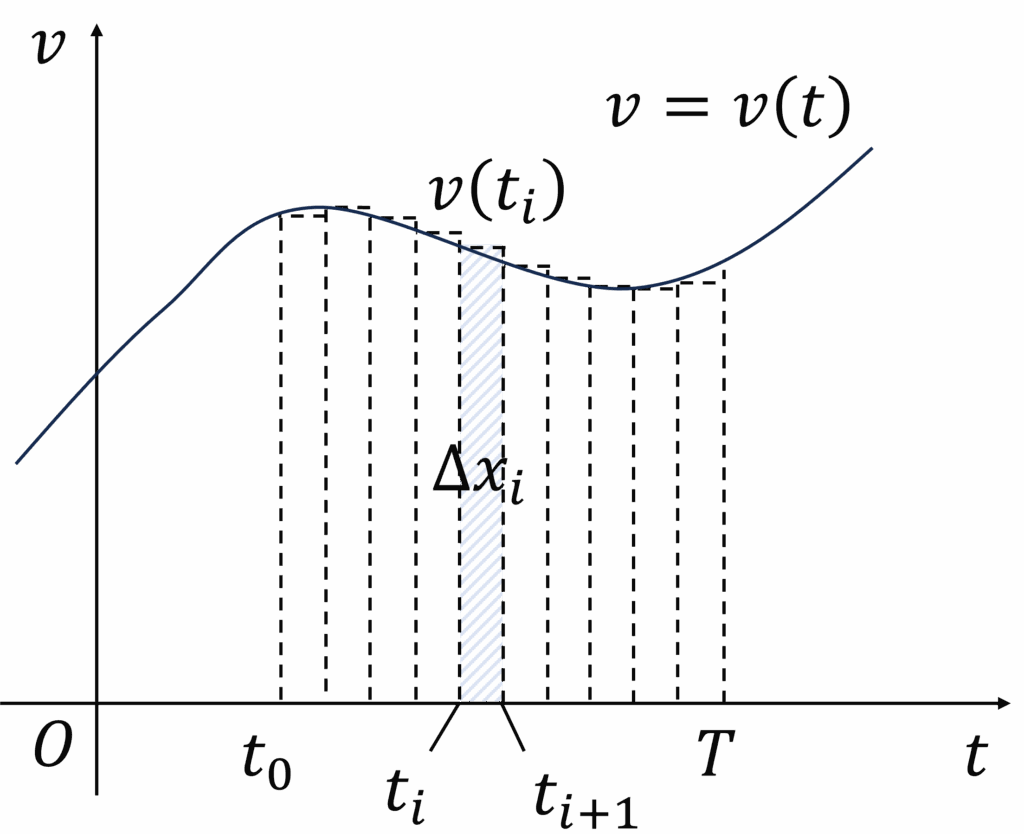
よって,この小さな長方形の総和として元の面積(変位)を近似的に求めることができると考えられます.つまり,図のように区間\(t=t_0~T\)を\(N\)等分すれば,所望の面積\(ΔX\)は小さな長方形の面積の総和\[ΔX≒Δx_0+Δx_1+Δx_2+・・・+Δx_i+Δx_{i+1}+・・・+Δx_{N-1}\]として求められます.具体的には,\(i\)番目のはじめの時刻を\(t_i\),おわりの時刻を\(t_{i+1}\)とすると,長方形1つあたりの横幅\(Δt\)は\[Δt=t_{i+1}-t_i=\frac{T-t_0}{N}\]と表せ,また\(t_i\)番目の長方形の高さは\(v(t_i)\)(一定)とみなせるので,その面積は\[Δx_i=v(t_i)Δt\]と表せます.よって,これを\(i=0~N-1\)まで足し合わせることにより,近似的に\(ΔX\)が求まります.すなわち\[ΔX≒\sum_{i=0}^{N-1} Δx_i=\sum_{i=0}^{N-1} v(t_i)Δt\]が成り立ちます.
上で求めた総和は,あくまで区間\(Δt\)のそれぞれで速度を一定とみなしたことによる近似値であり,これは図において長方形がはみ出していたり隙間が生じていることを見ても明らかです.この誤差を小さくするために,分割数\(N\)を大きく(すなわち区間幅\(Δt\)をできるだけ小さく)とることを考えます.すると,下図のように各長方形が細長くなり,誤差が小さくなります.
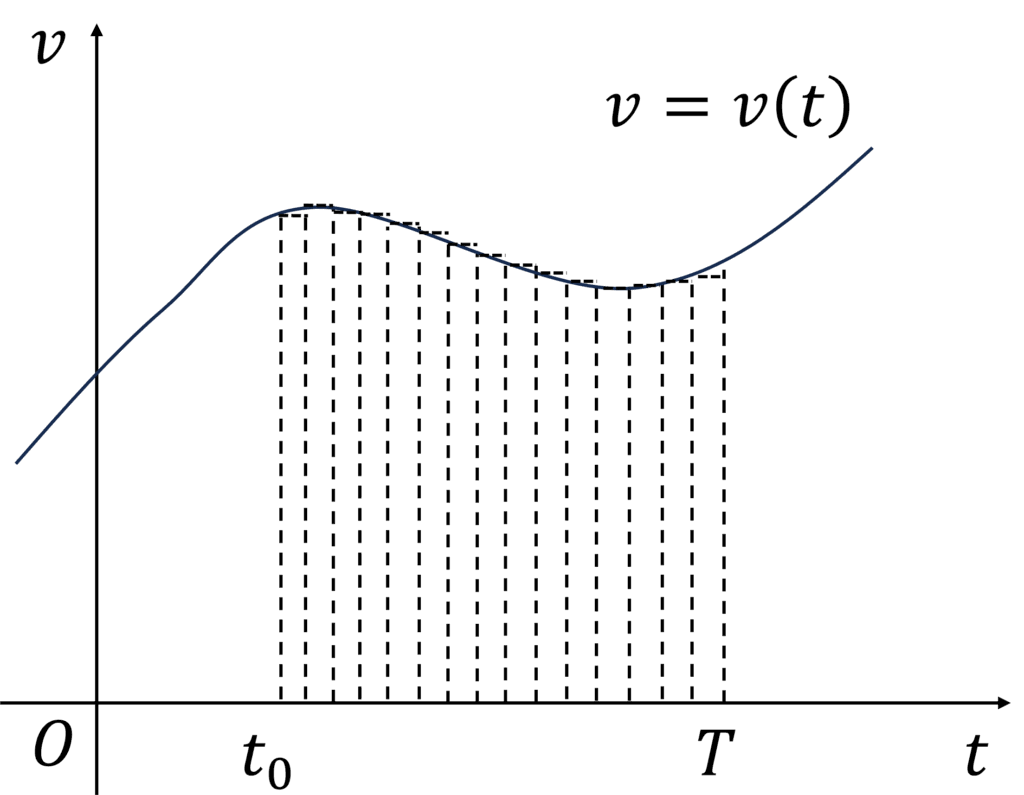
したがって,\(N→∞\)の極限をとれば,誤差は零とみなせ,上式は\(≒→=\)となります.すなわち\[ΔX=\lim_{N\to \ ∞} \sum_{i=0}^{N-1} Δx_i=\lim_{N\to \ ∞}\sum_{i=0}^{N-1} v(t_i)Δt\]が成り立ちます.これを定積分といい\[ΔX=\int_{t_0}^{T}dx=\int_{t_0}^{T}v(t)dt\]と表します.この導き方から分かるように,積分には変化する物理量の総量を微小量の総和として求める操作という意味合いがあります.また,位置\(x\)と速度\(v\)との間に\(v(t)=\frac{dx}{dt}\)という関係があるので\[ΔX=\int_{t_0}^{T}dx=\int_{t_0}^{T}\frac{dx}{dt}dt\]が成り立ち,操作としての微分と積分は互いに逆演算であるといえます.なお,上式より実用的に\(\frac{dx}{dt}\)を分数とみなし\(\frac{dx}{dt}dt=dx\)として約分のようにしてよく,物理学や工学ではしばしばこの考え方が用いられます.
また,ここで求めたのはある区間における面積(変位)という具体的な数値であったのに対して,区間を指定せずにある時刻\(t_c\)(任意定数)から任意の時刻\(t\)までの定積分を考えることにより導関数から元の関数を引き出すことができます.これを\[\int_{t_c}^{t}v(t)dt=\int v(t)dt=x(t)+C\qquad (Cは任意定数)\]と表し,これを不定積分といいます.ここで,導関数としての速度\(v(t)\)に対する位置\(x(t)\)を,速度の原始関数といい,任意定数\(C\)は定積分の下端を任意定数としたことによる原始関数の不定性を示しています.任意定数は積分定数とも呼ばれ,物理学的には積分下端における原始関数の値(これを初期値という)を意味します.
例えば,速度が\(v(t)=t^2\)で与えられたとき,時刻\(t=t_1\)から\(t_2\)までの変位は定積分の定義より\[ΔX=\lim_{N\to \ ∞}\sum_{i=0}^{N-1} v(t_i)Δt=\lim_{N\to \ ∞}\sum_{i=0}^{N-1} (t_1+iΔt)^2Δt\]\[=\lim_{N\to \ ∞}\sum_{i=0}^{N-1} (t_1^2+2t_1iΔt+i^2)Δt\]となるので,和を計算すると\[ΔX=\lim_{N\to \ ∞}\{Nt_1^2+2t_1\frac{N(N-1)Δt}{2}+\frac{N(N-1)(2N-1)(Δt)^2}{6}\}Δt\]となります.これより,極限を計算すれば\[ΔX=\frac{(t_2)^3-(t_1)^3}{3}\]を得ます.不定積分の場合も定義に従い,同様に\[x(t)=\int t^2dt=\frac{t^3}{3}+C\qquad (Cは任意定数)\]となります.このように,このように定義から求めることも大切ですが,内容が理解されたならば\[\int t^ndt=\frac{t^{n+1}}{n+1}+C\qquad (Cは任意定数,nは0以上の整数)\]あるいは\[\int_{t_1}^{t_2}v(t)dt=\left[ x(t) \right]_{t_1}^{t_2}\]
のような公式を活用して瞬時に微分できるようにする練習も必要です.