自然現象が生じるというのは,時間の変化に伴って物理量が変化していくことを言います.たとえば,物体の位置について,これが時間の経過(例えば\(1s,2s,3s\)…)に伴って\(1m,2m,3m…\)と変化したならば,この物体は移動していることが分かります.
より一般性を持たせるために,物体の位置を\(x\),時間を\(t\)という文字で代表することにします.いま,位置\(x\)が時間\(t\)に伴って変化するとき,数学的には位置は時間の関数であると言い\[x(t)\]と表します.実際には\[x(t)=at+b\]のような関数で与えられることになります.もちろん,現実の物理現象をこのようなきれいな式で表すことはできませんが,現象を理想化・単純化して近似的に考えることで,我々の知る様々な関数の組み合わせとして表現することができます.
さて,物理量の変化が表されたならば,新たな情報としてその変化率に興味があります.つまり,\(1s\)間に\(10m\)進むのと\(100m\)進むのでは,全く異なる運動が観察できるはずで.これを厳密に評価するには定量的(数値的)に表現する必要があります.そこで,一般に時間\(Δt\)(\(Δ\)は変化を表す記号)の間に位置が\(Δx\)変化したとき,位置の時間変化率として速度を\[v(t)=\frac{Δx(t)}{Δt}\]で定義すれば,速度を見ることにより,位置がどれくらい勢いよく変化しているかを定量的に知ることができます.このことをグラフで確認してみましょう.いま,物体1の速度が\(x=2t\),物体2の速度が\(x=\frac{1}{2}t\)で表されたとします.これらを\(x-t\)グラフに表すと
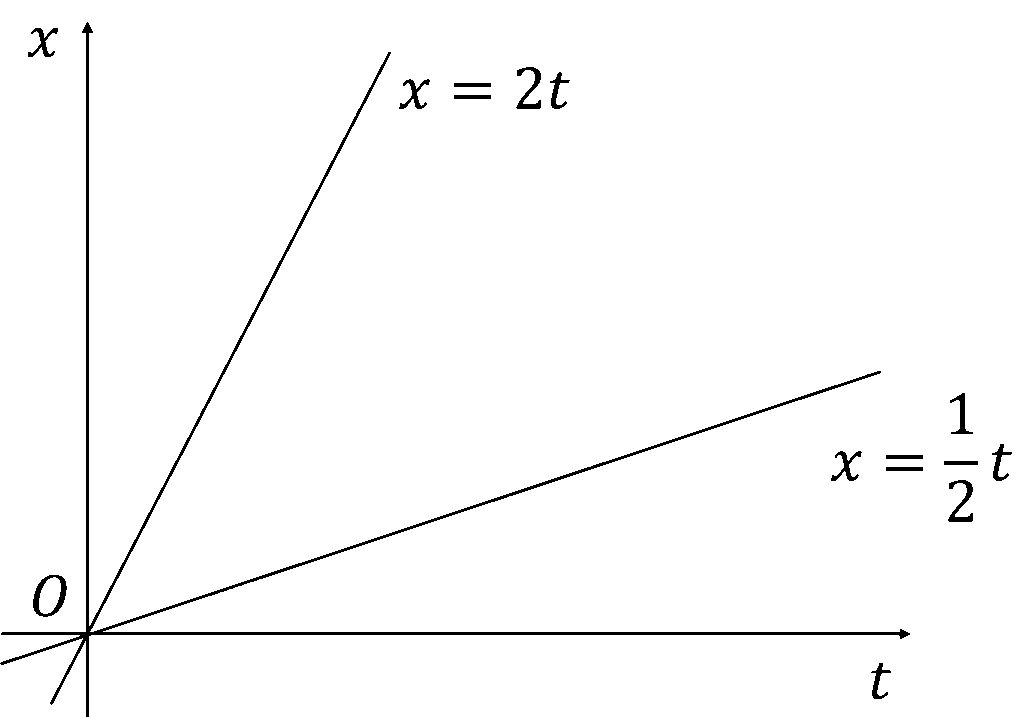
のようになります.ここで,それぞれの速度を考えると,これは(\(x\)の変化量)/(\(t\)の変化量)であるので,グラフの傾きを与えることになります.実際,物体1の速度は\(2\),物体2の速度は\(\frac{1}{2}\)となり,物体2よりも物体1のほうが速さが大きい=傾きが急であることが分かります.
上の例では位置が一次関数,すなわち傾き=速度一定であったため,速度は簡単に求められました.しかし,例えば下図のように傾き=速度が刻々と変化していく関数で与えられた場合,どうすればよいでしょうか.
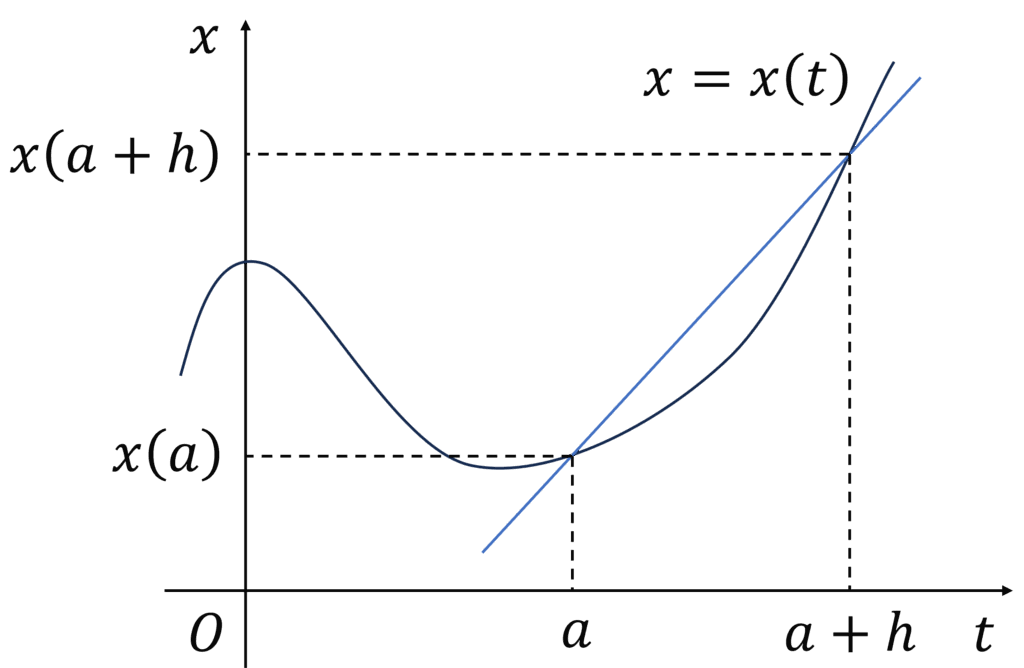
この場合も,まずは定義に従って速度を求めてみましょう.いま,一般に位置が\(x=x(t)\)と表されたとします.このとき,時刻\(t=a\)から\(t=a+h\)までの間に位置が\(x(a)\)から\(x(a+h)\)まで変化したとき,この間の速度は\[\overline{v(a,a+h)}=\frac{x(a+h)-x(a)}{h}\]と求められます.これは,図形的にはグラフにおける青い直線の傾きを意味します.しかし,図からもわかるようにこの区間内でも速度は刻々と変化しているので,上式は変化率としては良い指標にはなりません.
そこで,グラフがほぼ直線とみなせるまで,区間幅を小さくすればどうでしょうか.つまり,\(h\)を\(t=a\)に向けて限りなく0に近づけていくと,青い直線は最終的に時刻\(t=a\)における接線とほぼ近似できます.

もちろん,この際変化率を求めるという意味で\(h\)は0に限りなく近づけるだけで0にはなりません(0にすると傾きが定まらない).これは,数学的には\(\frac{x(a+h)-x(a)}{h}\)の\(h→0\)の極限をとると言い\[v(a)=\lim_{h\to \ 0} \overline{v(a,a+h)}=\lim_{h\to \ 0} \frac{x(a+h)-x(a)}{h}\]と表します.これを時刻\(t=a\)における位置の微分係数(時刻\(t=a\)における速度)と言い,図形的には\(t=a\)における接線の傾きを与えます.こうして,複雑な関数のある時刻における瞬間的な変化率(傾き)を得ることができました.
しかし,ここで求めた微分係数は,特定の時刻における瞬間変化率(傾き)を与えるだけで,関数全体の変化率(傾き)の情報を表現しているわけではありません.そこで関数全体の,おのおのの時刻\(t\)に対してその微分係数を対応させた関数\[v(t)=\lim_{h\to \ 0} \overline{v(t,t+h)}=\lim_{h\to \ 0} \frac{x(t+h)-x(t)}{h}\]を考えると,これは元の関数(\(x(t)\))の瞬間変化率を与える関数(\(v(t)\))となり,これを導関数といいます.またこのとき,\(h=Δt\),\(x(t+h)-x(t)=Δx\)とおくと,上式は\[v(t)=\lim_{Δt\to \ 0} \overline{v(t,t+Δt)}=\lim_{Δt\to \ 0} \frac{Δx}{Δt}=\frac{dx}{dt}\]と表せます.このときの\(dx\)および\(dt\)をそれぞれ\(x\)の微分および\(t\)の微分といい,上式の操作,すなわち導関数を求めることを「微分する」といいます.例えば,ある物体の位置が\[x(t)=2t^2+2t+1\]と与えられたとき,その速度(導関数)は\[v(t)=\frac{dx}{dt}=\lim_{Δt\to \ 0} \frac{\{2(t+Δt)^2+2(t+Δt)+1\}-\{2t^2+2t+1\}}{Δt}=4t+2\]となり,時刻\(t=2\)における速度(微分係数)は\[v(2)=10\]となります.このように定義から求めることも大切ですが,内容が理解されたならば\[\frac{d}{dt}(t^n)=nt^{n-1}\qquad nは整数\]のような公式を活用して瞬時に微分できるようにする練習も必要です.